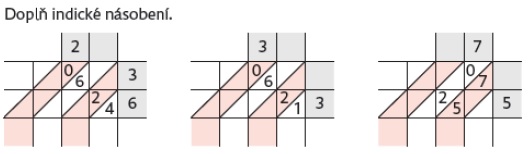
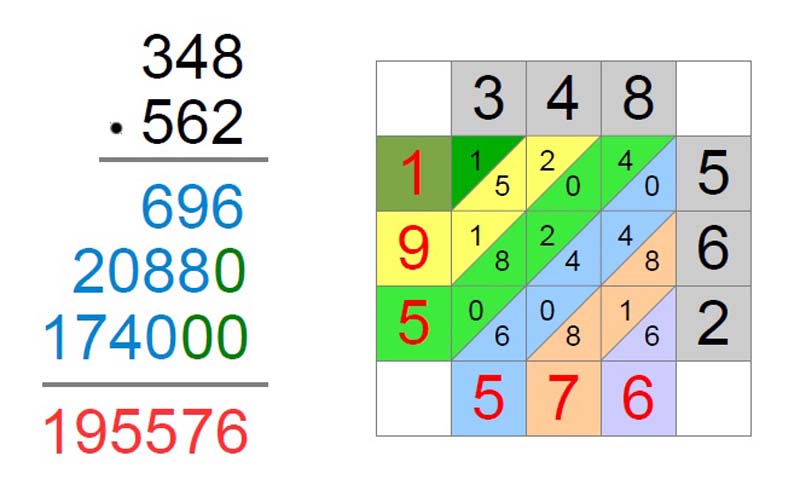
Proč indické násobení dříve nežli běžný algoritmus?

Je vidět celý násobek (snazší kontrola)

Jsou odděleny operace násobení a sčítání (výhoda nejen pro slabé žáky)

Lze tvořit úlohy na doplňování tabulek indického násobení (děti zároveň dělí)

Je motivující - děti baví

A hlavně - děti fascinuje, že jsou schopné vynásobit  velká čísla ("Ani tátovi na kalkulačce to nešlo").

A právě kvůli  násobení "obrčísel"  jsem narazila na problém s tabulkami. Grafický. Snažila jsem se jej řešit již při psaní učebnice pro čtvrtou třídu, ale bylo řečeno, že grafika se měnit nebude. A kde je tedy ten problém?

 V učebnicích je výsledek násobení  stažen do řádku a vznikají tak "hluchá" trojúhelníková pole.

A právě s prázdnými poli měla řada dětí  problém, byly zmatené a chtěly do nich "něco vyplňovat".

A co je ještě podstatnější - nedokázaly si takovou tabulku nakreslit a tím ani vytvořit vlastní úlohu!

Co s tím?

Já používám pro žáky daleko jednodušší variantu. Tabulku, kde jsou prázdná pouze rohová pole. Po barevných skluzavkách se čísla sčítají (od jednotek, s přechodem přes desítku).

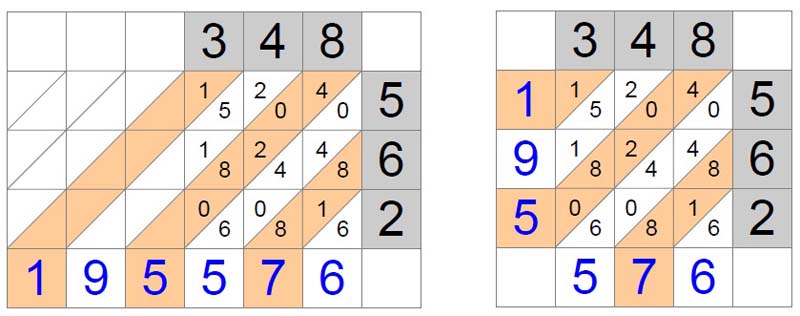
Porovnejte:

Výhody:

Děti si tabulku potřebnou k výpočtům nakreslí bez přemýšlení naprosto automaticky. Vědí, že vše má být vyplněné, pouze

rohy ne.  A že je výsledek "do obloučku" je ani v nejmenším nezaskočí.

Nevýhoda indického násobení?

Častým argumentem proti indickému násobení je to, že si děti musí kreslit tabulku. Kdo učí Hejného metodou ví, že to pro ně není ani ten nejmenší problém - klidně si ji načmárají na malý okraj sešitu, když potřebují rychle něco vypočítat.

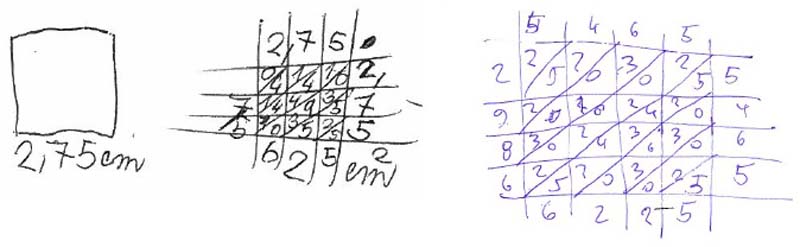
Všimněte si, že indicky násobí klidně i desetinná čísla - v ukázce vlevo počítali obsah čtverce o straně 2,75 cm.  Když tak Markétka v páté třídě začala počítat, překvapilo mě to a ptám se: "A jak víš, kolik desetinných míst ve výsledku máš oddělit?" Markéta: "Když nenapíšu čárku, tak mám nahoře číslo 100x větší, vpravo 100x menší. A když se vynásobí, tak je to 100 krát 100, 10000. Takže výsledek musím desetitisíckrát zmenšit." A bylo.

Barevnou tabulku mám zvětšenou a pověšenou na stěně, takže ji děti mají stále na očích i s běžným algoritmem (soubor). Věřím tomu, že kdybych ji nepoužívala, nepřinesl by mi Kryšpín po prvním seznámení s indickým násobením hned druhý den toto:

Zkuste přečíst výsledek!

EB_indické_násobení.pdf